Расчет устойчивости склонов
|
Расчет устойчивости склонов предлагается выполнять с использованием двух подходов: детерминированный и полувероятностный.
1. В детерминированном подходе характеристики грунта (удельный вес грунта, параметры прочности с и φ), определенные с учетом пространственной изменчивости при построении ЦИГМ, в модуле расчета устойчивости склонов осредняются в пределах каждого слоя грунта и принимаются постоянными в рассмотренных ниже методах расчета.
2. В полувероятностном подходе характеристики грунта, определенные с учетом пространственной изменчивости при построении ЦИГМ, в модуле расчета устойчивости склонов в пределах каждого слоя грунта принимаются переменными.
В обоих подходах рассмотрены методы расчета предложенные В.Феллениусом, А.Бишопом, Е.Спенсером, Н.Моргенштйном и В.Прайсом, Н.Янбу, Г.М. Шахунянцем и метод несбалансированных сил.
|
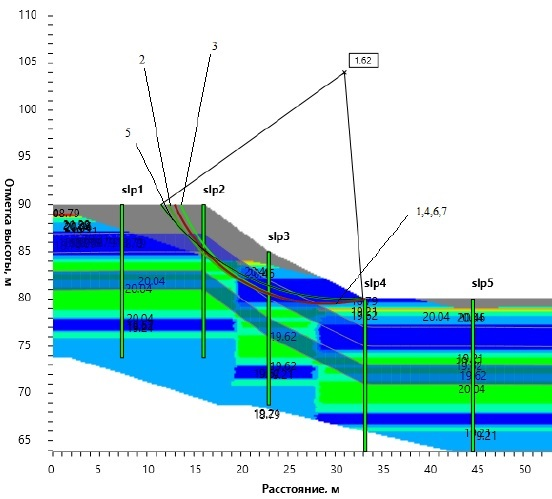
Предельные поверхности скольжения, найденные различными методам: 1 – Феллениус; 2 – Бишоп; 3 – Спенсер; 4 – Янбу; 5 – Моргенштерн-Прайс; 6 – Шахунянц; 7 – метод несбалансированных сил
|
|
Минимальное значение коэффициента устойчивости во всех методах расчета может быть найдено путем уменьшения параметров прочности до критического значения.
Вероятностный расчет устойчивости склонов выполняется методом Монте-Карло. Метод Монте-Карло (МК) основан на моделировании вероятности отказа Pf и индекса надежности β. Независимо от задачи, для решения которой используется MК, первым шагом является генерация случайных значений параметров прочности с нормальной или логнормальной функцией плотности вероятности и последующее решение одним из рассмотренных выше методов.
Для расчета Pf склонов с помощью вероятностного анализа, основанного на предельном равновесии, выполняется поиск критической поверхности скольжения и определяется минимальный коэффициент устойчивости, используя каждую реализацию параметров прочности грунта (силы удельного сцепления и/или угол внутреннего трения). Вероятность отказа определяется как отношение числа реализаций, у которых коэффициент устойчивости меньше единицы (k < 1), к общему числу реализаций (N).
|
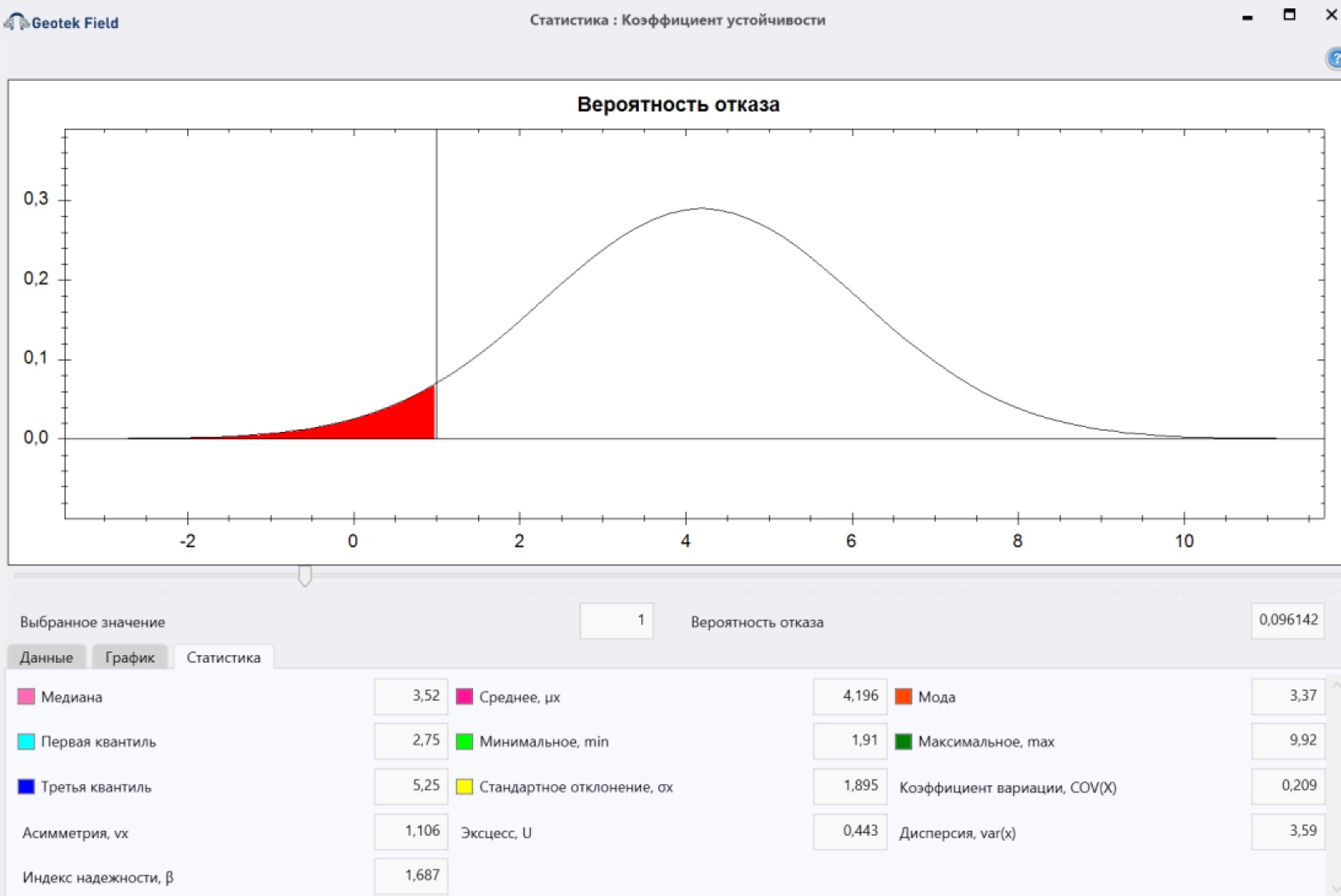
Вероятность отказа, индекс надежности и основные статистики
|
|
Моделирование методом Монте-Карло предлагает практический подход к анализу надежности, поскольку стохастический характер реакции системы (выходных данных) может быть вероятностно воспроизведен. С помощью этого метода можно определить свойства грунтов, таких как прочность грунта на сдвиг, исходя из их известного (или предполагаемого) распределения вероятностей. Для этой цели необходимо задать функцию плотности вероятности для каждого
параметра прочности (с и φ). Обычно для этих параметров предполагается нормальное распределение, а удельный вес грунта принимается как среднее значение. Затем рассчитывается соответствующий коэффициент устойчивости для каждого параметра прочности. Эти значения коэффициентов устойчивости отображаются на графике плотности вероятности, чтобы определить его вид распределения (нормальный или логнормальный). Индекс надежности β и вероятность отказа Pf затем рассчитываются с использованием распределения вероятности коэффициента устойчивости.
|
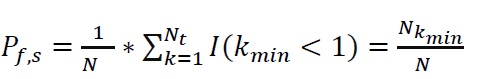
где 𝑁 – общее количество MК реализаций случайного поля; 𝑘𝑚𝑖𝑛 – значение коэффициента устойчивости менее единицы; I[.]- функция индикатор, которая равна 1 или 0, когда k < 1 или k ≥ 1, соответственно.
|
